Hi All,
When I started learning about the concept of reactive power it was a bit difficult to grasp, thanks to Chris' patient explanations I understood. Now I found this text, explained in a simple way, and thought it could be helpful for those learning the basics:
"What's the physical meaning of reactive power?
In electric circuits, some common misconceptions can make Reactive Power quite confusing. Before proceeding, first we have to fix our foundational ideas. For example:
With AC, the energy flows back and forth? Wrong. Only the electric charges flow back and forth, while the energy ideally goes in a single direction. (It’s a bit like sound waves versus wind. The air wiggles back and forth, while the sound waves move in a single direction. In circuits, the charges wiggle back and forth, while the energy goes in a single direction.)
Electricity is a form of energy? Wrong, the coulombs of electricity are not joules of energy. Electricity and energy are two entirely different things; two separate kinds of flow, and an ampere is not a watt. Important: the amperes are a very slow flow, while the watts are a light-speed flow. (Again, this is analogous to slow wind, versus fast sound waves, both in the same bit of atmosphere. Amps are the wind, watts are the propagating sound: waves versus medium.)
Electricity travels at the speed of light inside wires? Wrong. It's only the energy which travels at nearly the speed of light. At the same time, the electricity circulates quite slowly. Or with AC, the electricity wiggles back and forth. Electricity is the medium, and the Electrical Energy is the waves.
The energy comes out of the generator, flows through the light bulb filament, then returns to the generator? Nope, only the electricity does that; it flows in a closed circle without loss. Energy behaves very differently. Instead the energy comes out of the generator, travels rapidly along both halves of the circuit, then it gets absorbed by the light bulb filament. In the cord for a lamp or a blender, the energy zooms along both wires at the same time. In a 3-phase system the energy zips along all three wires in the same direction. Energy goes one-way, from source to load, while electricity travels in a complete loop and returns to its starting point. (It’s analogous to closed-loop hydraulics. The oil flows slowly in a circle, while the “horsepower” moves instantly through the system, zooming out of the pump, and making the distant hydraulic cylinders move instantly, without visible delay, even though the liquid moves slow.)
OK, then what is Reactive Power?
It’s simple. Reactive Power is when the ENERGY vibrates back and forth! Ha!
See why this can get confusing?
Usually the electricity wiggles, while the energy goes smoothly forward. If we believed that “electricity” was one single thing, then we’re screwed. We’ll never be able to understand. Or instead, if we wrongly imagine that electricity was a form of energy, or that the energy is always "alternating" in an AC system, then our concepts are completely distorted! In that case we'll never be able to grasp the concept of reactive power, or even truly understand basic electric circuits.
So, first we must attain a clear understanding of the two kinds of flows: the charge versus the energy, and to also understand how watts move along, versus the amperes.
The amps go sloooowly in a complete circle, moving like a drive-belt, or like a very long flywheel, while at the same time, the watts travel rapidly; traveling down both wires in the same direction, going at nearly light-speed. (Again, look at your oldschool AC desk lamp, and visualize that the energy is flowing along both wires, going from the wall-outlet to the light bulb, where it is absorbed by the hot filament.)
Rather than the Alternating Amperes, instead what happens when the energy starts going back and forth? This just means that electrical energy is "sloshing" to and fro between the AC generator and the distant loads. Normally this wave-energy flows smoothly in just one direction, going from the Utility Company to your washing machine. But instead, if the energy bounces back and forth between the separate ends of the power-grid, that just means you're not using up that energy. Instead you’re sending it all back to the generator.
This “energy-sloshing effect” is measured in watts of Reactive Power. If the energy all reflects back to the power company, that’s pure 100% reactive power. But if instead your light bulbs are using up electric energy, with none bouncing back, that’s purely “Real Power.”
Capacitors can set up this "energy sloshing" situation, if used as the load.
Capacitors ideally draw only Reactive Power. When connected to a dynamo, they don't constantly absorb electrical energy, as with heaters and motors. Instead capacitors charge up …and then discharge again. They bounce all the energy back to the source. (Coils as loads will ideally do the same thing: filling up and then emptying, reflecting the energy back to the distant AC dynamo.) If we plug our capacitor into a wall-outlet, then ideally all the electrical energy which is going into the capacitor ...goes right back out again, and returns to the distant AC source. Then repeat! Charge up your capacitor, then discharge it back into the distant dynamos. (Actually this happens twice per complete cycle of AC, where the energy sloshes at 120Hz rather than 60Hz. For energy transfer, the polarity doesn’t matter, and your load-capacitor stores some energy on the positive AC cycle, and again on the negative. Twice per cycle.)
An ideal coil does almost the same thing. Connect it to the AC source, and first it becomes “charged” with a large current and magnetic field, then it “discharges” again, where the field collapses and the energy gets sent back to the dynamo. Then it does it all again, on the opposite AC half-cycle.
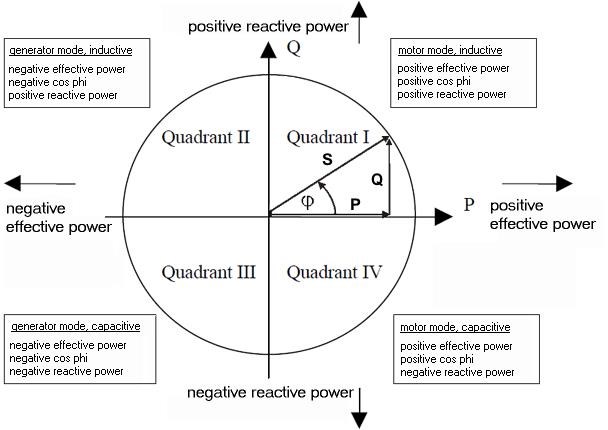
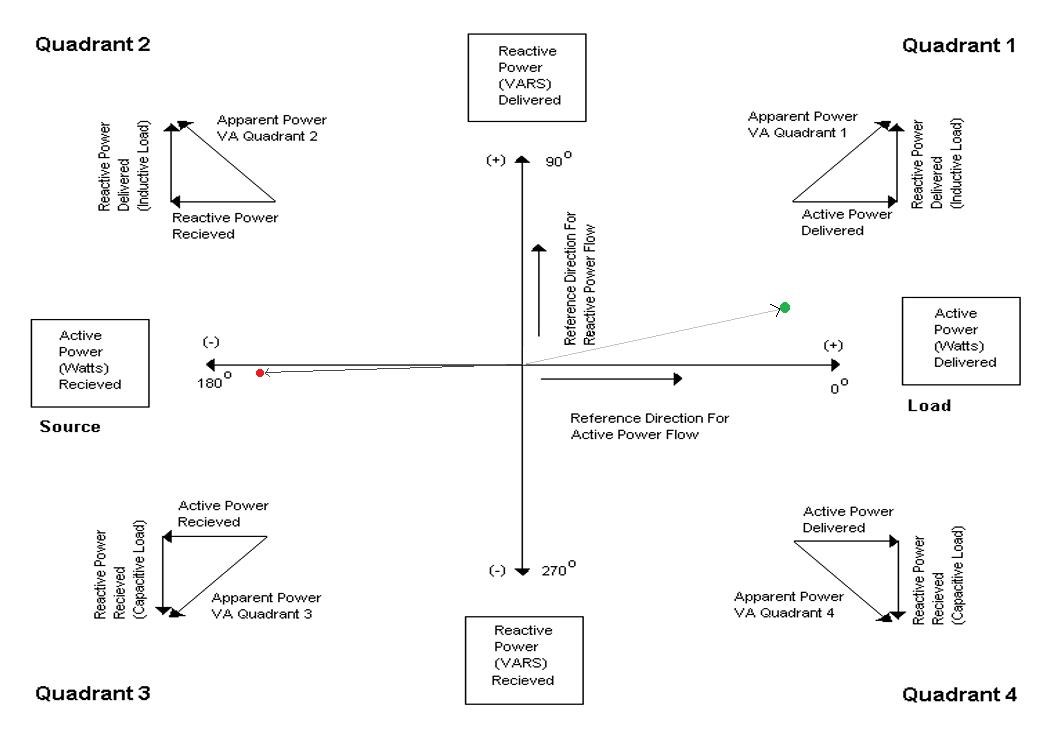
On the other hand, "Real Power” means that energy goes one-way only, from source to load. We have to pay someone for real power. "Reactive Power” means that energy goes back and forth only, with none being absorbed. "Complex Power" is just the sum of the two effects, with some energy being genuinely absorbed by the load, but part of it being bounced back to the dynamos again.
Pure resistors draw Real Power only: the one-way energy-flow. Pure capacitors (and coils) draw Reactive Power only, where the energy-waves all “slosh back” to the distant dynamo.
OK, where do these effects appear in the AC mathematics? If we start graph-plotting the sine-waves of voltage and current, jthen ust where do we see this “energy-sloshing” effect? The answer is actually straightforward.
In a lamp-cord or other 2-wire transmission line, if the voltage and current are in synch (zero phase difference,) then the electrical energy is traveling in a single direction, call it right-to-left. (Imagine powering a flashlight bulb with a battery, but then reverse the battery terminals. The energy still flows in the same direction, going to the bulb!)
Now instead if the current is 180deg out of phase with the voltage, then still the energy is traveling in a single direction, but backwards. It flows smoothly left-to-right.
These changes between 0deg and 180deg are reversing the average long-term direction of energy-flow.
What would happen if the phase-delay between volts and amps wasn’t zero, and also wasn’t 180deg? Yep, you guessed it. That’s when the energy starts wiggling back and forth. With a small phase-shift between the voltage and the current, then for each AC half-cycle, the direction of watts reverses twice, first forwards, then back, then repeat.
And finally, if the phase-delay is exactly 90deg, or exactly -90deg (270deg,) that means we have “purely sloshing” with no net energy flow at all. At those values of phase-delay, every bit of the energy that traveled right-to-left, is sent back again, left-to-right. These special angles are seen whenever we use ideal capacitors and ideal inductors as our load. Neither of these components use any net energy. But they sure do “slosh” energy around, first a “charge” then followed by a “discharge.” Coils and capacitors …it’s almost as if they were the same component! Capacitors store energy as e-fields, inductors store energy as b-fields. In capacitors, the stored energy is related to the voltage, in the coil its related to the current. Capacitors cause a 90deg phase lead, the coils a 90deg phase lag. (Capacitors, they’re just coils which have somehow been turned inside-out!)
It’s all simple, really. Once you can see it in your mind. The serious complexity appears when both inductors and capacitors are present, or we start adding resistors into the mix, all with phase-lags which aren’t exactly -90deg, 180deg, etc. (“Complexity.” Heh.)
And finally, notice that there’s nothing imaginary about any of this. Reactive power has nothing to do with imaginary flows, and everything to do with “energy-sloshing” flows. [I think “imaginary numbers” was a terrible name for them. They should have been called “sideways numbers” or something less misleading. “Contrary numbers,” so that a capacitor would be drawing “contrary watts” from the AC grid, instead of “imaginary” watts!]"
By William Beatty